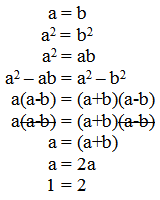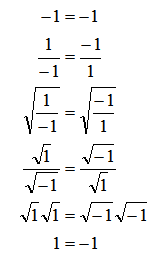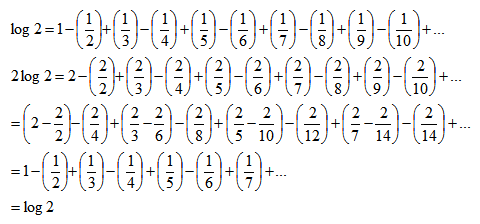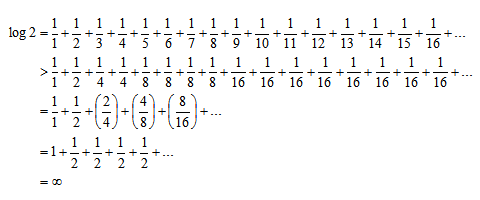I’ve seen many proofs that 1=2. Here’s a classic.
The (not-so-subtle) error in the above proof is that we’re cancelling (a-b) on both sides, when (a-b) equals zero. That is, we’re dividing by zero on both sides. That completely invalidates the equality.
Another proof uses the fact that the square root of a number can be both positive or negative.
(Proving -1=1 is the same as proving 1=2. Once you have one wrong proof, you can prove every other falsehood.)
The flaw here is that the square root of 1 is 1 and -1. So right after the square root symbol appears, every equation should have a plus-or-minus symbol on both sides.
The most convincing proof uses absolutely convergent series as the key idea. Here’s how the proof goes.
Most people initially think that the flaw is in the re-arrangement of the series. That’s not true! The re-arrangement works just fine, and you can prove that every term is correct to infinity.
The flaw is subtler.
When an infinite series is summed, it can be summed in any order. But the total may vary depending on the order you sum it up! You are guaranteed that the total is the same only if the series is absolutely convergent. That is, if the sum of the absolute values of each number is finite. (See the Wikipedia article on the Riemann series theorem.)
For the log 2 series, it’s not absolutely convergent. The series diverges, as shown below:
So, by re-arranging the series for log 2, we’ve invalidated the equality anyway.
This fact once saved an entire class. We had a problem in our first year physics course to which the answer was the series above. (It had to do with calculating the electromagnetic potential created by an array of charges.) Since the series is not absolutely convergent, and every possible answer was correct, the whole class got marks for this question, as long as they attempted it.